

 ','..','$myPermit') ?>
SYLLABUS Previous: Introduction
Up: Contents
Next: 2.1 Explicit 2 levels
','..','$myPermit') ?>
SYLLABUS Previous: Introduction
Up: Contents
Next: 2.1 Explicit 2 levels
The finite difference (FD) method is often used when a function
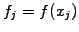 sampled on a homogeneous mesh
sampled on a homogeneous mesh
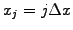 satisfies
a differential equation that can simply be approximated with
finite difference quotients (1.4.2#eq.2).
In explicit schemes, the solution is calculated directly in terms
of known quantities: explicit schemes are usually easy to implement in
a program, but more delicate to execute.
Implicit schemes are more robust at execution, but result in more
complicated codes solving a linear system: this can be slow in 2 or
higher dimensions and is then often advantageous to reconsider a more
general finite elements solution on an inhomogeneous mesh.
satisfies
a differential equation that can simply be approximated with
finite difference quotients (1.4.2#eq.2).
In explicit schemes, the solution is calculated directly in terms
of known quantities: explicit schemes are usually easy to implement in
a program, but more delicate to execute.
Implicit schemes are more robust at execution, but result in more
complicated codes solving a linear system: this can be slow in 2 or
higher dimensions and is then often advantageous to reconsider a more
general finite elements solution on an inhomogeneous mesh.


 ','..','$myPermit') ?>
SYLLABUS Previous: Introduction
Up: Contents
Next: 2.1 Explicit 2 levels
','..','$myPermit') ?>
SYLLABUS Previous: Introduction
Up: Contents
Next: 2.1 Explicit 2 levels