5.2 Stochastic theory

SYLLABUS Previous: 5.1 Monte Carlo integration Up: 5 MONTE-CARLO METHOD Next: 5.3 Particle orbits

5.2 Stochastic theory

Slide : [ mean & variance - normal - uniform - Wiener - Ito || VIDEO login]

This section is intended as a very short introduction into the stochastic theory, which provides the mathematical foundation behind the Monte Carlo method; check Sczepessy [28], Kloeden [22] and Van Kampen [20] for complete courses on the subject.

To begin, remember the definition of an expected or mean value $\mathcal{E}$ and the variance $\mathcal{V}$

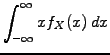$\displaystyle \mathcal{E}[X](x) \triangleq$	$\displaystyle \int_{-\infty}^{\infty}xf_X(x)\,dx$	(1)
$\displaystyle \mathcal{V}[X](x) \triangleq$	$\displaystyle \, \mathcal{E}\left[X\right]\left(\left(x- \mathcal{E}[X]\left(x\right)\right)^2\right)$	(2)
$\displaystyle =$	$\displaystyle \mathcal{E}\left[X\right]\left(x^2\right) - \mathcal{E}^2\left[X\right](x)$	(3)

where

is the density distribution function of a stochastic variable

. The notation $\mathcal{N}(\mu,\sigma)$ refers to the set of Gaussian or normally distributed stochastic variable

with a density distribution function

$\displaystyle f_X(x)=\frac{1}{\sigma\sqrt{2\pi}} \exp\left[-\frac{(x-\mu)^2}{2\sigma^2}\right]$

(4)

where $\mu$ is the mean and $\sigma^2$ is the variance. Along the same lines, $\mathcal{U}(a,b)$ stands for the set of uniformly distributed random numbers in the interval

Now consider a class of stochastic processes that play a central role in the Monte Carlo method: is called a Wiener process (or in an equivalent manner Brownian motion) at a time if and only if

$W_{t+\Delta t}-W_t \;\in \mathcal{N}(0,\sqrt{\Delta t})$ , where $\mathcal{N}$ is the set of normal distributed random numbers.
$\mathcal{E}[W_tdW_t]=\mathcal{E}[W_t]\mathcal{E}[dW_t]$ , where $\mathcal{E}$ denotes expected value, $dW_t=W_{t+\Delta t}-W_t$ and $\Delta t>0$ , i.e. the Wiener increment is independent of the past.

It turns out that the distribution of Wiener increments $W_{t+\Delta t}-W_t$ is essentially the same function as the Green's function of the diffusion equation (1.3.2#eq.3).

The differential calculus of stochastic processes (or Itô calculus) involves new properties that are fundamentally different from the ordinary (or Riemann) calculus. The reason can be tracked down to the preferred direction of time in the Itô integral, which is defined as the limit of the explicit (forward Euler) discretization

$\displaystyle \int_0^T b(W_t,t)\circ dW_t \equiv \sum_i \lim_{\Delta t_i\rightarrow 0} b(W_{t_i},t_i) (W_{t_i+\Delta t_i} - W_{t_i})$

(5)

for any sequence $\{ t_i:t_i \in [0,T], t_{i+1}=t_i+\Delta t_i \}$ . Note that the circle $\circ$ here stands for Itô differential and states that

is independent of

; also, an implicit discretization in (5.2#eq.5) would give a fundamentally different result.

Define a property that is a sum of a Riemann and an Itô integral

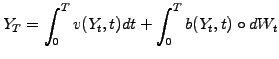$\displaystyle Y_T=\int_0^T v(Y_t,t) dt + \int_0^T b(Y_t,t)\circ dW_t$

(6)

For an infinitely short time interval, this leads to the stochastic differential equation

$\displaystyle dY_t= v(Y_t,t) dt + b(Y_t,t)\circ dW_t$

(7)

which reduces to an ordinary differential equation in the absence of the stochastic component

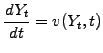$\displaystyle \frac{dY_t}{dt}= v(Y_t,t)$

(8)

Stochastic differential equations such as (5.2#eq.7) are used in the Monte-Carlo method to describe the trajectories or orbits of particles.

SYLLABUS Previous: 5.1 Monte Carlo integration Up: 5 MONTE-CARLO METHOD Next: 5.3 Particle orbits