

 ','..','$myPermit') ?>
SYLLABUS Previous: 5.2 Stochastic theory
Up: 5 MONTE-CARLO METHOD
Next: 5.4 A scheme for
','..','$myPermit') ?>
SYLLABUS Previous: 5.2 Stochastic theory
Up: 5 MONTE-CARLO METHOD
Next: 5.4 A scheme for
5.3 Particle orbits
Slide : [
deterministic -
Taylor -
stochastic -
Feynman-Kac ||
VIDEO
99) echo "
modem -
ISDN -
LAN
"; else echo "login";?>
]
In the Monte Carlo method, the initial condition or indeed any function is
discretized using quasi-particles; differential
operators are therefore reformulated in terms of particle motions.
Remember that a quasi-particle is defined in (1.4.7#eq.1)
by a weight 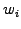 , a position
, a position 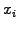 and a shape function
and a shape function 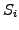 ; for
simplicity, we assume here unit weights
; for
simplicity, we assume here unit weights 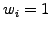 and point shaped particles
in the form of Dirac pulses
and point shaped particles
in the form of Dirac pulses
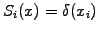 . The solution can then be
calculated from the particles density obtained from the positions
. The solution can then be
calculated from the particles density obtained from the positions
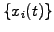 called particle orbits. By construction, the lowest
order moment is perfectly conserved, since no particle is lost.
called particle orbits. By construction, the lowest
order moment is perfectly conserved, since no particle is lost.
To show the contrast between the Taylor and the Feynman-Kac
theorems, which provide a rigorous foundation for the Monte Carlo method,
the deterministic and the stochastic motion are first
considered separately.
 Deterministic orbits
Deterministic orbits
- satisfy an ordinary differential equation for
the position
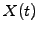 as a function of time
as a function of time 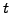
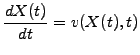 |
(1) |
or
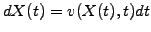 |
(2) |
This is solved numerically using the methods discussed in section 1.2.1, using an explicit or implicit discretization of time
For an ensemble of 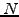 particles with orbits
particles with orbits 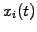 , the particle
density distribution function
, the particle
density distribution function 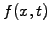 is obtained by superposition
is obtained by superposition
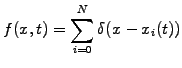 |
(4) |
and is plotted in the applet below using the
projection (1.4.7#eq.3) from section 1.4.
JBONE applet: press Start/Stop
to simulate the deterministic motion of a particle or random walker
(red dot).
The contribution to the density distribution (black line) is obtained
from a linear assignment of the position on a coarse grid.
|
|
"; ?>
If a large number of particles approximate a smooth density function
and each individual orbit 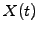 evolves in a deterministic manner
evolves in a deterministic manner
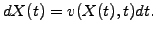 |
(5) |
then the Taylor's transport theorem states that the evolution of
the particle density distribution function 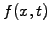 satisfies the
advection equation
satisfies the
advection equation
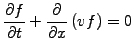 |
(6) |
The theorem makes it possible to study a PDE instead of an
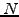 -particle system; the reverse is also true and will be used to
solve the advection equation with particles.
-particle system; the reverse is also true and will be used to
solve the advection equation with particles.
 Stochastic particle orbits
Stochastic particle orbits
- are defined as an ensemble of possible
orbits with different probabilities. Imagine a snowflake falling slowly
from the sky: the motion is unpredictable and each evolution can be
described with an orbit
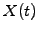 following the stochastic differential
equation
following the stochastic differential
equation
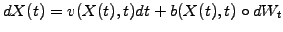 |
(7) |
where 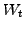 is a Wiener processes (Brownian motion). Averaging over
a large number of orbits, the average velocity and the broadening of
possible orbits are readily obtained (exercise 5.02) as
is a Wiener processes (Brownian motion). Averaging over
a large number of orbits, the average velocity and the broadening of
possible orbits are readily obtained (exercise 5.02) as
Stochastic orbits can therefore be parametrized with statistical averages
 } \circ d{W}_t$](s5img70.gif) |
(10) |
and lead to a different result each time the JBONE applet is
executed.
JBONE applet: press Start/Stop
to simulate the random motion of a particle (red dot).
The contribution to the density distribution (black line) is obtained
from a linear assignment of the position on a grid.
|
|
"; ?>
In the same spirit as in Taylor's transport theorem, it is possible to
relate the evolution of a large number of stochastic particle orbits to
a PDE; the so-called Feynman-Kac theorem tells that a smooth
density distribution function 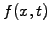 in which individual particles
move according to
in which individual particles
move according to
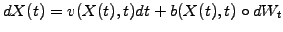 |
(11) |
evolves according to the Fokker-Planck equation
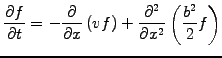 |
(12) |
which is in fact an advection-diffusion equation.
For example, let 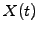 be a stochastic process with an evolution of the
probability density distribution
be a stochastic process with an evolution of the
probability density distribution 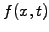 following the advection-diffusion
equation
following the advection-diffusion
equation
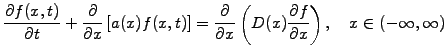 |
(13) |
From the Feynman-Kac theorem, it is easy to show (exercise 5.01) that
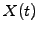 satisfies the stochastic differential equation
satisfies the stochastic differential equation
showing exactly what evolution is required to reproduce statistically the
properties desired at the macroscopic scale.
SYLLABUS Previous: 5.2 Stochastic theory
Up: 5 MONTE-CARLO METHOD
Next: 5.4 A scheme for


 ','..','$myPermit') ?>
SYLLABUS Previous: 5.2 Stochastic theory
Up: 5 MONTE-CARLO METHOD
Next: 5.4 A scheme for
','..','$myPermit') ?>
SYLLABUS Previous: 5.2 Stochastic theory
Up: 5 MONTE-CARLO METHOD
Next: 5.4 A scheme for
![]() , a position
, a position ![]() and a shape function
and a shape function ![]() ; for
simplicity, we assume here unit weights
; for
simplicity, we assume here unit weights ![]() and point shaped particles
in the form of Dirac pulses
and point shaped particles
in the form of Dirac pulses
![]() . The solution can then be
calculated from the particles density obtained from the positions
. The solution can then be
calculated from the particles density obtained from the positions
![]() called particle orbits. By construction, the lowest
order moment is perfectly conserved, since no particle is lost.
called particle orbits. By construction, the lowest
order moment is perfectly conserved, since no particle is lost.
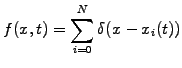
![]() evolves in a deterministic manner
evolves in a deterministic manner
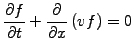
![]() in which individual particles
move according to
in which individual particles
move according to
![]() be a stochastic process with an evolution of the
probability density distribution
be a stochastic process with an evolution of the
probability density distribution ![]() following the advection-diffusion
equation
following the advection-diffusion
equation