previous up next ','..','$myPermit') ?> SYLLABUS  Previous: 1.4.4 Splines  Up: 1.4 Numerical discretization  Next: 1.4.6 Wavelets


1.4.5 Harmonic functions

A harmonic decomposition is obtained from a discrete Fourier transform (DFT) assuming a regular mesh and a periodic domain of length $ L$ . Using the notations $ x_m=m\Delta x=m L/M$ and $ k_m=2\pi m /L$ , the forward and backward transformations are defined as

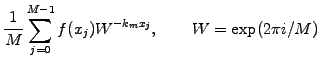$\displaystyle \widehat{f}(k_m)$ $\displaystyle =$ $\displaystyle \frac{1}{M}\sum_{j=0}^{M-1} f(x_j) W^{-k_m x_j},\quad\quad W=\exp(2\pi i/M)$ (1.4.5#eq.1)
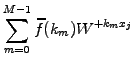$\displaystyle f(x_j)$ $\displaystyle =$ $\displaystyle \sum_{m=0}^{M-1} \widehat{f}(k_m) W^{+k_m x_j}$ (1.4.5#eq.2)

If $ M$ is a power of 2, the total number of operations can be dramatically reduced from $ 8M^2$ to $ M\log_2 M$ in a fast Fourier transform (FFT), by applying recursively the decomposition
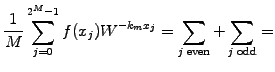$\displaystyle \widehat{f}(k_m)$ $\displaystyle =$ $\displaystyle \frac{1}{M}\sum_{j=0}^{2^M-1} f(x_j) W^{-k_m x_j} = \sum_{j\;\mathrm{even}} +\sum_{j\;\mathrm{odd}} =$  
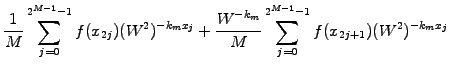  $\displaystyle =$ $\displaystyle \frac{1}{M}\sum_{j=0}^{2^{M-1}-1} f(x_{2j}) (W^2)^{-k_m x_j} +\frac{W^{-k_m}}{M}\sum_{j=0}^{2^{M-1}-1} f(x_{2j+1})(W^2)^{-k_m x_j}$  

with $ W^2=\exp(2i\pi/2^{M-1})$ until a sum of DFT of length $ M=2$ is obtained. Figure (1.4.5#fig.1) illustrates how the approximation of a periodic square wave converges with an increasing number of Fourier components. Note how the function overshoots in the neighborhood of sharp edges: this is the Gibbs phenomenon and it will always be there for a finite number of terms in the sum.

Figure: Square wave $ \displaystyle\sum_{m=0}^M \frac{2}{\pi(2m+1)}\sin\left(\frac{(2m+1)\pi x}{L}\right)$ with $ M=3,6,12$ .
\includegraphics[width=10cm]{figs/AprxFFT.psc}

It should not be surprizing to hear that a harmonic decomposition is particularly well suited for smooth global functions with long wavelengths $ \lambda\sim L$ , since they result in a narrow spectrum $ \vert k\vert\le 2\pi/\lambda\ll \pi/\Delta x$ . Note that the convergence with an increasing number of Fourier components is faster than any polynomial once the smallest structure has been resolved. The implementation of non-periodic boundary conditions, however, can sometimes be problematic.

SYLLABUS  Previous: 1.4.4 Splines  Up: 1.4 Numerical discretization  Next: 1.4.6 Wavelets