previous up next ','..','$myPermit') ?> SYLLABUS  Previous: 1.4.5 Harmonic functions  Up: 1.4 Numerical discretization  Next: 1.4.7 Sampling with quasi-particles


1.4.6 Wavelets

Starting with a coarse (global) approximation, the idea behind wavelets is to successively refine the representation and store the difference from one scale to the next

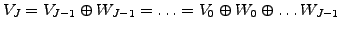$\displaystyle V_J = V_{J-1}\oplus W_{J-1} = \hdots = V_0 \oplus W_0 \oplus \hdots W_{J-1}$ (1.4.6#eq.1)

This is best illustrated with Haar wavelets in figure (1.4.6#fig.1), showing that the piecewise constant approximation at a level V4 can be brought to the higher level V5 by adding a correction W4.
Figure: Successive approximation of 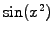$ \sin(x^2)$ using Haar wavelets.
\includegraphics[width=10cm]{figs/AprxWAW.psc}
Appropriate for integral equations and best suited for the understanding, Haar wavelets are however not practical for the evaluation of derivatives in PDEs. In the spirit of the FFT, Mrs Daubechies proposed a fast $ \mathcal{O}(N)$ linear discrete wavelet transformation (DWT) called DAUB4
$\displaystyle \left[\begin{array}{rrrrrrrrrrr} c_0 & c_1 & c_2 & c_3 & & & & & ... ...ts \\ \tilde{g_1}\\ \tilde{g_2}\\ \tilde{g_3}\\ \tilde{g_4} \end{array}\right]$       
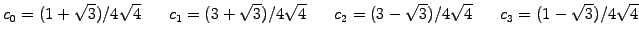$\displaystyle c_0=(1+\sqrt{3})/4\sqrt{4} \hspace{7mm} c_1=(3+\sqrt{3})/4\sqrt{4} \hspace{7mm} c_2=(3-\sqrt{3})/4\sqrt{4} \hspace{7mm} c_3=(1-\sqrt{3})/4\sqrt{4}$    
    (1.4.6#eq.2)

which is applied successively to the function 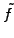$ \tilde{f}$ together with the permutation until only the first two components remain. The inverse is calculated by reversing the procedure and using the inverse matrix
$\displaystyle \left[\begin{array}{c} f_1 \\ f_2 \\ f_3 \\ f_4 \\ \vdots \\ f_5... ...ts \\ \tilde{g_1}\\ \tilde{g_2}\\ \tilde{g_3}\\ \tilde{g_4} \end{array}\right]$    
    (1.4.6#eq.3)

Approximations with DAUB4 have the peculiar property that the derivative exists almost everywhere. Even if wavelets are not smooth, they still can represent exactly piecewise polynomial functions of arbitrary slope - the cusps in the wavelets cancel out exactly! 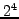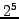Figure (1.4.6#fig.2) illustrates how the solution converges when the first $ 2^4$ DWT components of DAUB4 $ [\sin(x^2)]$ are taken to a higher level of refinement with $ 2^5$ components.

Figure: Successive approximation of 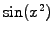$ \sin(x^2)$ using DAUB4 wavelets.
\includegraphics[width=10cm]{figs/AprxDWT.psc}

Apart from Haar and Daubechies wavelets, a whole family can be generated with a cascading process that is nicely illustrated in the Wavelet Cascade Applet. Wavelets are still relatively new and remain a matter of active research [29]: they have been proven useful in approximation theory, but are still being developed both for differential and integral equations. Clearly apparent in the figures (1.4.6#fig.1) and (1.4.6#fig.2) is the difficulty of incorporating the boundary conditions. Another issue that will become clear in the coming sections, is the difficulty of calculating overlap integrals.

SYLLABUS  Previous: 1.4.5 Harmonic functions  Up: 1.4 Numerical discretization  Next: 1.4.7 Sampling with quasi-particles