

 ','..','$myPermit') ?>
SYLLABUS Previous: 1.2.1 Ordinary differential equations
Up: 1.2 Differential Equations
Next: 1.2.3 Boundary / initial conditions
','..','$myPermit') ?>
SYLLABUS Previous: 1.2.1 Ordinary differential equations
Up: 1.2 Differential Equations
Next: 1.2.3 Boundary / initial conditions
1.2.2 Partial differential equations
Slide : [ PDE
second order -
splitting ||
VIDEO
99) echo "
modem -
ISDN -
LAN
"; else echo "login";?>
]
Partial differential equations (PDE) involve at least 2 variables in space
(boundary value problems) or time (initial value problems).
The equation is called second order if there are not more than two
derivatives acting on the same unknown function 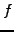
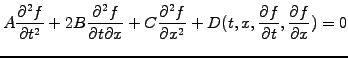 |
(1.2.2#eq.1) |
It is linear if  is linear in
is linear in  , and is homogeneous if
all the terms in
, and is homogeneous if
all the terms in 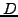 depend only on
depend only on 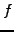 .
Initial value problems involving a combination of linear and non-linear
operators
.
Initial value problems involving a combination of linear and non-linear
operators
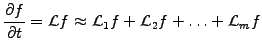 |
(1.2.2#eq.2) |
can often be solved with an operator splitting.
The idea, based on the separation of variables, is to decompose the
operator into a linear combination with 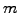 independent terms and to
solve the problem in sub-steps where each part is evolved separately
while keeping all the others fixed.
Non-linearities are often split from linear terms that can be treated
with the special techniques shown in this course (e.g. exercise 6.04).
Multi-dimensional problems can sometimes be solved using a linear
splitting called alternating-direction implicit (ADI), where only one
spatial dimension is evolved at a time using an implicit scheme.
independent terms and to
solve the problem in sub-steps where each part is evolved separately
while keeping all the others fixed.
Non-linearities are often split from linear terms that can be treated
with the special techniques shown in this course (e.g. exercise 6.04).
Multi-dimensional problems can sometimes be solved using a linear
splitting called alternating-direction implicit (ADI), where only one
spatial dimension is evolved at a time using an implicit scheme.
SYLLABUS Previous: 1.2.1 Ordinary differential equations
Up: 1.2 Differential Equations
Next: 1.2.3 Boundary / initial conditions


 ','..','$myPermit') ?>
SYLLABUS Previous: 1.2.1 Ordinary differential equations
Up: 1.2 Differential Equations
Next: 1.2.3 Boundary / initial conditions
','..','$myPermit') ?>
SYLLABUS Previous: 1.2.1 Ordinary differential equations
Up: 1.2 Differential Equations
Next: 1.2.3 Boundary / initial conditions
![]()