

 ','..','$myPermit') ?>
SYLLABUS Previous: 1.2.2 Partial differential equations
Up: 1.2 Differential Equations
Next: 1.2.4 Characteristics and dispersion
','..','$myPermit') ?>
SYLLABUS Previous: 1.2.2 Partial differential equations
Up: 1.2 Differential Equations
Next: 1.2.4 Characteristics and dispersion
1.2.3 Boundary / initial conditions
Slide : [ BC/IC
intial conditions -
boundary conditions ||
VIDEO
99) echo "
modem -
ISDN -
LAN
"; else echo "login";?>
]
Depending on the problem, initial conditions (IC)
 |
(1.2.3#eq.1) |
and / or boundary conditions (BC) need to be imposed. The latter are
often of the form
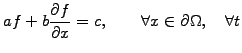 |
(1.2.3#eq.2) |
and are called Dirichlet (b=0), Neumann (a=0), or
Robin (c=0) conditions.
Other forms include the periodic condition
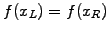 with
{
with
{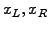 }
}
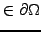
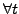 , and the outgoing-wave
conditions if the domain is open.
To prevent reflections from the computational boundary of an open domain,
it can be useful to introduce absorbing boundary conditions: the
implementation depends on the numerical method that is being used, but
typically model small layers of artificial material that absorbs the
outgoing wave using a few mesh cells.
Perfectly matched layers (PML) [4] are particularly
useful for electromagnetic wave problems and will be discussed in
conjunction with the leap-frog method (exercise 2.08).
, and the outgoing-wave
conditions if the domain is open.
To prevent reflections from the computational boundary of an open domain,
it can be useful to introduce absorbing boundary conditions: the
implementation depends on the numerical method that is being used, but
typically model small layers of artificial material that absorbs the
outgoing wave using a few mesh cells.
Perfectly matched layers (PML) [4] are particularly
useful for electromagnetic wave problems and will be discussed in
conjunction with the leap-frog method (exercise 2.08).
SYLLABUS Previous: 1.2.2 Partial differential equations
Up: 1.2 Differential Equations
Next: 1.2.4 Characteristics and dispersion


 ','..','$myPermit') ?>
SYLLABUS Previous: 1.2.2 Partial differential equations
Up: 1.2 Differential Equations
Next: 1.2.4 Characteristics and dispersion
','..','$myPermit') ?>
SYLLABUS Previous: 1.2.2 Partial differential equations
Up: 1.2 Differential Equations
Next: 1.2.4 Characteristics and dispersion