

 ','..','$myPermit') ?>
SYLLABUS Previous: 1.2.3 Boundary / initial conditions
Up: 1.2 Differential Equations
Next: 1.2.5 Moments and conservation
','..','$myPermit') ?>
SYLLABUS Previous: 1.2.3 Boundary / initial conditions
Up: 1.2 Differential Equations
Next: 1.2.5 Moments and conservation
1.2.4 Characteristics and dispersion relations
Slide : [ characteristics
elliptic -
parabolic -
hyperbolic || local
dispersion relation ||
VIDEO
99) echo "
modem -
ISDN -
LAN
"; else echo "login";?>
]
The characteristics of a PDE can loosely be defined as the trajectories
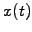 along which discontinuities and the initial conditions propagate:
think of the path a heat pulse takes in an inhomogeneous material.
The chain rule can be used more formally to classify second order
equations (1.2.2#eq.1) with D=0 using an ansatz
along which discontinuities and the initial conditions propagate:
think of the path a heat pulse takes in an inhomogeneous material.
The chain rule can be used more formally to classify second order
equations (1.2.2#eq.1) with D=0 using an ansatz
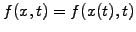
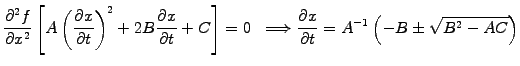 |
(1.2.4#eq.1) |
Three categories of equations depend on the sign of the discriminant:
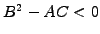 the equation has no characteristic and
is called elliptic (Laplace eq.)
the equation has no characteristic and
is called elliptic (Laplace eq.)
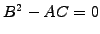 the equation has one characteristic and
is called parabolic (heat eq.)
the equation has one characteristic and
is called parabolic (heat eq.)
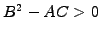 the equation has two characteristics and
is called hyperbolic (wave eq.)
the equation has two characteristics and
is called hyperbolic (wave eq.)
The characteristics play an important role and will be exploited in the
Lagrangian methods in chapter 6.
The local properties of a linear equation are conveniently investigated
by introducing the harmonic ansatz
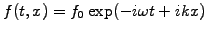 ,
which transforms differential operators in
,
which transforms differential operators in  into algebraic
expression in
into algebraic
expression in
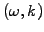 . In effect, you substitute
. In effect, you substitute
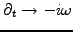 and
and
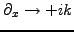
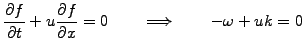 |
(1.2.4#eq.2) |
to produce a dispersion relation (or Von Neuman stability
relation), relating the PHYSICAL phase velocity
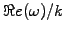 or
the growth rate
or
the growth rate
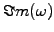 to the typical scale of the solution
to the typical scale of the solution 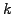 .
Assuming a homogeneous grid in space
.
Assuming a homogeneous grid in space
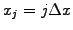 and time
and time
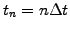 , it is moreover possible to assess the quality of the
numerical approximation, by relating the effective NUMERICAL phase
velocity or growth rate (i.e. obtained after discretization) to the
the spatial
, it is moreover possible to assess the quality of the
numerical approximation, by relating the effective NUMERICAL phase
velocity or growth rate (i.e. obtained after discretization) to the
the spatial 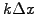 or temporal resolutions
or temporal resolutions
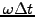 .
.
For example, take the effective wavenumber
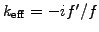 that results when the mid-point rule (1.2.1#eq.3) is used to
approximate the first derivative of the spatial function
that results when the mid-point rule (1.2.1#eq.3) is used to
approximate the first derivative of the spatial function
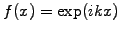 :
:
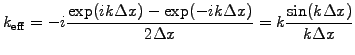 |
(1.2.4#eq.3) |
The wave number is under-estimated for poor resolution
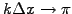 and even changes sign with less than
two mesh points per wavelength. The forward difference (1.2.1#eq.2)
and even changes sign with less than
two mesh points per wavelength. The forward difference (1.2.1#eq.2)
![$\displaystyle k_\mathrm{eff}=-i\frac{\exp(ik\Delta x) -1}{\Delta x} = k \frac{\...
...s\left(\frac{k\Delta x}{2}\right) +i\sin\left(\frac{k\Delta x}{2}\right)\right]$](s1img66.gif) |
(1.2.4#eq.4) |
has an imaginary part, showing that small wavelengths
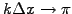 will be strongly damped
will be strongly damped
![$ f\propto \exp[-\Im m(k_\mathrm{eff})\Delta x]$](s1img67.gif) .
.
SYLLABUS Previous: 1.2.3 Boundary / initial conditions
Up: 1.2 Differential Equations
Next: 1.2.5 Moments and conservation


 ','..','$myPermit') ?>
SYLLABUS Previous: 1.2.3 Boundary / initial conditions
Up: 1.2 Differential Equations
Next: 1.2.5 Moments and conservation
','..','$myPermit') ?>
SYLLABUS Previous: 1.2.3 Boundary / initial conditions
Up: 1.2 Differential Equations
Next: 1.2.5 Moments and conservation
![]() along which discontinuities and the initial conditions propagate:
think of the path a heat pulse takes in an inhomogeneous material.
The chain rule can be used more formally to classify second order
equations (1.2.2#eq.1) with D=0 using an ansatz
along which discontinuities and the initial conditions propagate:
think of the path a heat pulse takes in an inhomogeneous material.
The chain rule can be used more formally to classify second order
equations (1.2.2#eq.1) with D=0 using an ansatz
![]()
![]() ,
which transforms differential operators in
,
which transforms differential operators in ![]() into algebraic
expression in
into algebraic
expression in
![]() . In effect, you substitute
. In effect, you substitute
![]() and
and
![]()
![]() that results when the mid-point rule (1.2.1#eq.3) is used to
approximate the first derivative of the spatial function
that results when the mid-point rule (1.2.1#eq.3) is used to
approximate the first derivative of the spatial function
![]() :
: