','..','$myPermit') ?>
SYLLABUS Previous: 6 LAGRANGIAN METHOD
Up: 6 LAGRANGIAN METHOD
Next: 6.2 Cubic-Interpolated Propagation (CIP)
','..','$myPermit') ?>
SYLLABUS Previous: 6 LAGRANGIAN METHOD
Up: 6 LAGRANGIAN METHOD
Next: 6.2 Cubic-Interpolated Propagation (CIP)
6.1 Splitting advection from the rest
Slide : [
Characteristics ||
VIDEO
99) echo "
modem -
ISDN -
LAN
"; else echo "login";?>
]
Start by splitting the entire evolution into a sequence of alternating
advection and non-advection phases
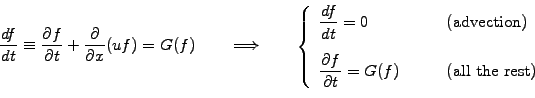 |
|
|
(1) |
The advection part (including the convective derivative) is first evolved by
propagating the solution along the characteristics; this
is achieved using a Lagrangian method such as the explicit cubic-interpolated
propagation (CIP) scheme, which is explicit and has no restriction on the
time step.
After this interpolation from the characteristics back to Eulerian coordinates,
the second non-advection part can then be solved using one of the methods that
have been discussed previously.


 ','..','$myPermit') ?>
SYLLABUS Previous: 6 LAGRANGIAN METHOD
Up: 6 LAGRANGIAN METHOD
Next: 6.2 Cubic-Interpolated Propagation (CIP)
','..','$myPermit') ?>
SYLLABUS Previous: 6 LAGRANGIAN METHOD
Up: 6 LAGRANGIAN METHOD
Next: 6.2 Cubic-Interpolated Propagation (CIP)