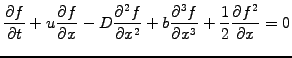 |
(1) |


 ','..','$myPermit') ?>
SYLLABUS Previous: 4.3 Aliasing, filters and
Up: 4 FOURIER TRANSFORM
Next: 4.5 Computer quiz
','..','$myPermit') ?>
SYLLABUS Previous: 4.3 Aliasing, filters and
Up: 4 FOURIER TRANSFORM
Next: 4.5 Computer quiz
Combining the linear terms from advection (1.3.1#eq.1), diffusion (1.3.2#eq.1), dispersion (1.3.3#eq.1) and the non-linear wave-breaking term (1.3.4#eq.1) into a single non-linear equation, yields
keepFFT to store the current values of spectrum
toolFFT for the transformation
to X-space required by the convolution and the plotting.
As mentioned earlier in sect.4.2, the sign of time in
(4.4#eq.3) has been changed to stick to the definition of the
phase factor used in
Numerical Recipes
[24].
int N = mesh_.size(); //A power of 2
double boxLen = mesh_.size()*mesh_.interval(0); //Periodicity
double k = 2*Math.PI/boxLen; //Notation
Complex ik1 = new Complex( 0., k );
Complex ik2 = new Complex(-k*k, 0. );
Complex ik3 = new Complex( 0.,-k*k*k);
Complex advection = new Complex(ik1.scale(velocity)); //Variables
Complex diffusion = new Complex(ik2.scale(diffusCo));
Complex dispersion= new Complex(ik3.scale(disperCo));
//----- Non-linear term: convolution
s = keepFFT.getFromKSpace(FFT.bothParts,boxLen); //Current Spectrum
toolFFT = new FFT(s,s,FFT.inKSpace); // for convolution
if (scheme.equals(jbone.ALIASED)) //With-/out aliasing,
sp = toolFFT.aliasedConvolution(boxLen); // use an FFT to
else //scheme.equals(jbone.EXPAND) // calculate product,
sp = toolFFT.expandedConvolution(boxLen); // FFT back to KSpace
//----- Linear terms: complex terms in spectrum s
s = keepFFT.getFromKSpace(FFT.bothParts,boxLen); //Current Spectrum
linear= s[0];
sp[0]=linear;
for (int m=1; m<=N/2; m++) {
total= advection.scale((double)(m ));
total=total.add(diffusion.scale((double)(m*m)));
total=total.add(dispersion.scale((double)(m*m*m)));
exp=(total.scale(timeStep)).exp();
linear = s[m].mul(exp);
nonlin = sp[m].mul(ik1.scale(0.5*timeStep*(double)(m)));
sp[m ] = linear.add(nonlin);
if (m<N/2) sp[N-m] = sp[m].conj(); //For a real spectrum
}
keepFFT = new FFT(sp,FFT.inKSpace); //Spectrum is complete
toolFFT = new FFT(sp,FFT.inKSpace); //inv FFT for plotting
f=toolFFT.getFromXSpacePart(FFT.firstPart,boxLen);
Depending on the scheme selector, the convolution is either calculated
without precaution
(subject to aliasing) or by temporarily
expanding the spectrum
by padding the upper part with zeros (cures the problem).
The example below shows the evolution obtained for the Korteweg-DeVries equation, when two solitons propagate and collide through the delicate balance between the non-linear wave-breaking and dispersion.
Replace the dispersion with a small amount of diffusion by setting
Dispersion=0.0 and Diffusion=0.1; evolve a Gaussian into
a shock front and verify how much less aliasing seems to be an issue
for the Burger equation (1.3.4#eq.2), when a
diffusive process physically damps the short wavelengths...
Remember however that the cascade of energy from one wavelength to
another is now affected by the aliasing and is much more delicate
to diagnose.
SYLLABUS Previous: 4.3 Aliasing, filters and Up: 4 FOURIER TRANSFORM Next: 4.5 Computer quiz