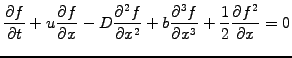previous up next ','..','$myPermit') ?> SYLLABUS  Previous: 4.3 Aliasing, filters and  Up: 4 FOURIER TRANSFORM  Next: 4.5 Computer quiz


4.4 Non-linear equations.

Slide : [ Scheme - Code - Run || VIDEO 99) echo " modem - ISDN - LAN "; else echo "login";?> ]

Combining the linear terms from advection (1.3.1#eq.1), diffusion (1.3.2#eq.1), dispersion (1.3.3#eq.1) and the non-linear wave-breaking term (1.3.4#eq.1) into a single non-linear equation, yields

$\displaystyle \frac{\partial f}{\partial t} + u\frac{\partial f}{\partial x} - ... ...ac{\partial^3 f}{\partial x^3} + \frac{1}{2}\frac{\partial f^2}{\partial x} = 0$ (1)

where the last term has been written so as to explicitly show the quadratic non-linearity. After transformation to Fourier space, all the spatial operators become algebraic and an ordinary evolution equation is obtained for each individual Fourier component

$\displaystyle \frac{d \widehat{f_m}}{dt} + (ik_m u +k_m^2D -ik_m^3b) \widehat{f_m} + \frac{1}{2}ik_m\widehat{f^2_m} = 0$ (2)

It would here of course be formally possible to write the non-linear term as a convolution in K-space, but it is much easier to write and more efficient to compute the multiplication in X-space. Following the same lines as in sect.4.2, the linear terms are integrated analytically and yield a phase shift proportional to the time-step $ \Delta t$ . The convolution is calculated numerically by transforming back and forth from Fourier to configuration space. A simple Euler integration (1.2.1#eq.2) in time yields the formal solution

$\displaystyle \widehat{f_m}^{t+\Delta t} = \widehat{f_m}^t\exp[-(ik_m u +k_m^2D -ik_m^3b)\Delta t] + \frac{\Delta t}{2}ik_m\widehat{f^2_m}^t$ (3)

This has been implemented in JBONE using the variable keepFFT to store the current values of spectrum $ \widehat{f_m}^t$ and the variable toolFFT for the transformation to X-space required by the convolution and the plotting. As mentioned earlier in sect.4.2, the sign of time in (4.4#eq.3) has been changed to stick to the definition of the phase factor used in Numerical Recipes [24]. 

      int N         = mesh_.size();                      //A power of 2
      double boxLen = mesh_.size()*mesh_.interval(0);    //Periodicity
      double   k    = 2*Math.PI/boxLen;                  //Notation
      Complex ik1   = new Complex(  0.,  k  );
      Complex ik2   = new Complex(-k*k,  0.  );
      Complex ik3   = new Complex(  0.,-k*k*k);

      Complex advection = new Complex(ik1.scale(velocity));  //Variables
      Complex diffusion = new Complex(ik2.scale(diffusCo));
      Complex dispersion= new Complex(ik3.scale(disperCo));


      //----- Non-linear term: convolution
      s  = keepFFT.getFromKSpace(FFT.bothParts,boxLen);  //Current Spectrum
      toolFFT = new FFT(s,s,FFT.inKSpace);               //  for convolution


      if (scheme.equals(jbone.ALIASED))                  //With-/out aliasing,
        sp = toolFFT.aliasedConvolution(boxLen);         //  use an FFT to
      else //scheme.equals(jbone.EXPAND)                 //  calculate product,
        sp = toolFFT.expandedConvolution(boxLen);        //  FFT back to KSpace
 
     //----- Linear terms: complex terms in spectrum s
      s = keepFFT.getFromKSpace(FFT.bothParts,boxLen);   //Current Spectrum
      linear= s[0];
      sp[0]=linear;
      for (int m=1;  m<=N/2;  m++) {
        total=          advection.scale((double)(m ));
        total=total.add(diffusion.scale((double)(m*m)));
        total=total.add(dispersion.scale((double)(m*m*m)));
        exp=(total.scale(timeStep)).exp();
        linear    = s[m].mul(exp);
        nonlin    = sp[m].mul(ik1.scale(0.5*timeStep*(double)(m)));
        sp[m  ]   = linear.add(nonlin);
        if (m<N/2) sp[N-m] = sp[m].conj();               //For a real spectrum
      }

      keepFFT = new FFT(sp,FFT.inKSpace);                //Spectrum is complete
      toolFFT = new FFT(sp,FFT.inKSpace);                //inv FFT for plotting
      f=toolFFT.getFromXSpacePart(FFT.firstPart,boxLen);
Depending on the scheme selector, the convolution is either calculated without precaution (subject to aliasing) or by temporarily expanding the spectrum by padding the upper part with zeros (cures the problem).

The example below shows the evolution obtained for the Korteweg-DeVries equation, when two solitons propagate and collide through the delicate balance between the non-linear wave-breaking and dispersion.
JBONE applet:  press Start/Stop to simulate the collision between two solitons, here first computed using an expanded convolution to avoid the aliasing from the quadratic non-linearity in the Korteweg-DeVries (KdV) equation.
"; if ($user_nbr<100) echo " "; echo "

"; ?>



Numerical experiments: non-linear equations with FFT
  1. Change the switch to Aliased Convolution and observe how aliasing pollutes the spectrum with short wavelengths that evolve into a non-linear instability.
  2. Go back to the KdV equation by setting Dispersion=0.5 and try to cure the aliased scheme with a small amount of non-physical diffusion. Separate the short wavelengths (unphysical aliases) from the longer wavelengths (physical) by reducing the ICAmplitude. Is such a solution attractive?

Replace the dispersion with a small amount of diffusion by setting Dispersion=0.0 and Diffusion=0.1; evolve a Gaussian into a shock front and verify how much less aliasing seems to be an issue for the Burger equation (1.3.4#eq.2), when a diffusive process physically damps the short wavelengths... Remember however that the cascade of energy from one wavelength to another is now affected by the aliasing and is much more delicate to diagnose.

SYLLABUS  Previous: 4.3 Aliasing, filters and  Up: 4 FOURIER TRANSFORM  Next: 4.5 Computer quiz