

 Previous: Ad-hoc complex resistivity
Up: GLOBAL MODES & DAMPING
Next: CONCLUSIONS
Previous: Ad-hoc complex resistivity
Up: GLOBAL MODES & DAMPING
Next: CONCLUSIONS
By now, it should be clear that a consistent description of the coupling
between a fluid AE and the kinetic-Alfvén wave requires a gyrokinetic
description of the passing bulk ions with FLR corrections at least to
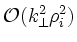 .
This has first been derived in Ref.[37] and implemented in
the PENN code [8]. The perturbed current contributes
mainly along the magnetic field and can be written symbolically using
the dispersion function1
.
This has first been derived in Ref.[37] and implemented in
the PENN code [8]. The perturbed current contributes
mainly along the magnetic field and can be written symbolically using
the dispersion function1
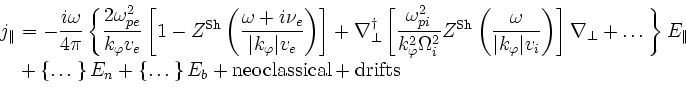 |
(7) |
The second order term
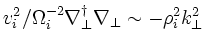 ,
reproduces the FLR induced kinetic-Alfvén wave dispersion (eq.1)
with the real part of the second dispersion function. In addition, a number of
terms are not shown here and contribute in a non-evident manner to account for
the proper amount of mode conversion in toroidal geometry.
The expression shows explicitly how the resistive damping (collision
frequency
,
reproduces the FLR induced kinetic-Alfvén wave dispersion (eq.1)
with the real part of the second dispersion function. In addition, a number of
terms are not shown here and contribute in a non-evident manner to account for
the proper amount of mode conversion in toroidal geometry.
The expression shows explicitly how the resistive damping (collision
frequency  in the imaginary part of the first dispersion function)
differs from the selective Landau damping (
in the imaginary part of the first dispersion function)
differs from the selective Landau damping (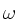 in the imaginary part
of the second dispersion function).
Most important compared with the previous models,
is that the Landau damping is here proportional to the electrostatic
component
in the imaginary part
of the second dispersion function).
Most important compared with the previous models,
is that the Landau damping is here proportional to the electrostatic
component 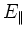 :
solving Maxwell's equations for an Alfvénic perturbation
:
solving Maxwell's equations for an Alfvénic perturbation
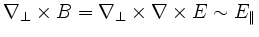 with the spatial scale self-consistently described with FLR effects, this
reproduces the selective damping
with the spatial scale self-consistently described with FLR effects, this
reproduces the selective damping
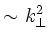 from (eq.2)
that affects mainly the shorter wavelength kinetic-Alfvén wave.
To perform analytically the integration over the resonant denominators
from (eq.2)
that affects mainly the shorter wavelength kinetic-Alfvén wave.
To perform analytically the integration over the resonant denominators
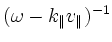 and formulate a differential problem in both
the radial and poloidal directions, the wave-particle resonance has
been approximated assuming passing particles and using a functional
dependence for the parallel wave vector, e.g.
and formulate a differential problem in both
the radial and poloidal directions, the wave-particle resonance has
been approximated assuming passing particles and using a functional
dependence for the parallel wave vector, e.g.
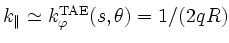 .
This approximation can be tested a posteriori in two manners:
Except for DKAE modes where the mode conversion takes place to an
electromagnetic drift wave [15,38] and depends rather
sensitively on the choice of
.
This approximation can be tested a posteriori in two manners:
Except for DKAE modes where the mode conversion takes place to an
electromagnetic drift wave [15,38] and depends rather
sensitively on the choice of 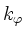 ,
these self-consistency
checks largely justify the approximations made.
They show that the global damping of AEs depends mainly on the location
where the conversion occurs, which determines how much power is converted
and finally deposited by the kinetic Alfvén wave. In other words, the
global damping of AEs depends only weakly on the local Landau damping
that affects only the distance the wave covers before it is ultimately
damped.
,
these self-consistency
checks largely justify the approximations made.
They show that the global damping of AEs depends mainly on the location
where the conversion occurs, which determines how much power is converted
and finally deposited by the kinetic Alfvén wave. In other words, the
global damping of AEs depends only weakly on the local Landau damping
that affects only the distance the wave covers before it is ultimately
damped.
The strength of our approach is that it does not a priori rely on any
particular mode conversion mechanism that has been mocked-up from an
informed guess; following the dispersion and damping of both the fast
and slow global wavefields, mode conversion spontaneously occurs where
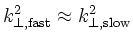 .
Five conversion mechanisms have been found so far, of which four occur to
the kinetic Alfvén wave and only two had been expected from heuristic
arguments. They are illustrated in the sketch of Fig.3:
.
Five conversion mechanisms have been found so far, of which four occur to
the kinetic Alfvén wave and only two had been expected from heuristic
arguments. They are illustrated in the sketch of Fig.3:
Figure 3:
Sketch of four mode conversion mechanisms between the fluid (MHD)
and kinetic Alfvén (KAW) wavefields.
|
|
- 1.
- Near the plasma center, where the aspect ratio is large and the shear
is sufficiently weak, the kinetic-Alfvén wave expands radially until
it matches the global fluid scale [31].
This mechanism reproduces the global AE dampings measured in a set of
similar JET discharges, showing with (eq.2) that the
gyrokinetic mode structure correctly changes with the isotope mass
[11].
- 2.
- Within gaps, mode conversion sometimes reduces to radiative damping
if the kinetic-Alfvén wave is damped in the vicinity of this gap,
so that both models reproduce the global damping measurements from
JET to a good degree of accuracy [31,35].
Global effects within a single gap can however also split a weakly
damped AE into KAEs [14,41], couple adjacent gaps to
form high-n global KAE [38] and the fast particles may even
drive the kinetic Alfvén wave [38].
- 3.
- At Alfvén resonances, mode conversion is generally not as efficient
as continuum damping. The wavefield and damping predicted by the
PENN and CASTOR-K codes have been compared with
measurements from JET in Ref.[30,31] showing clear
contradictions with continuum damping model.
- 4.
- In the plasma edge, the large magnetic shear associated with the
plasma shaping (X-point) squeezes the wavefield radially and
triggers a mode conversion. The strong global damping rate that
results has been tested in the time evolution of Ref.[31].
- 5.
- Mode conversion to electromagnetic drift waves becomes possible
in the neighborhood of rational surfaces where
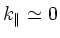 if
if
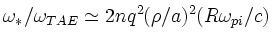 approaches unity, so that drift-kinetic AEs (DKAEs) become unstable.
They provide for a plausible mechanism for the instabilities observed
in the TAE frequency range of DIII-D [42,15];
their modeling is however likely to suffer from the approximative
treatment of the parallel dynamics with
approaches unity, so that drift-kinetic AEs (DKAEs) become unstable.
They provide for a plausible mechanism for the instabilities observed
in the TAE frequency range of DIII-D [42,15];
their modeling is however likely to suffer from the approximative
treatment of the parallel dynamics with
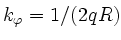 .
.
So far, the gyrokinetic PENN model with approximate parallel
dynamics is the only tool that deals properly with the mode conversion
of global wavefields in a tokamak; most toroidal predictions remain
therefore to be confirmed using other models.
The KIN-2DEM code [9] from PPPL/Princeton does not
presently retain the dynamics of passing ions and therefore misses the
mode conversion to kinetic-Alfvén wave that is essential for AEs and
perhaps also important for kinetic ballooning modes (KBM).
A gyrokinetic model including the main ingredients has recently been
formulated in Ref.[43] and might be implemented in a future
version of the NOVA code.
A model for electromagnetic micro-instabilities is currently under
development at CRPP/Lausanne for low 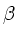 plasmas in simple toroidal
geometry and includes the parallel dynamics of passing and trapped bulk
particles to all orders in
plasmas in simple toroidal
geometry and includes the parallel dynamics of passing and trapped bulk
particles to all orders in
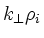 [46];
the model retains the mode conversion both to the kinetic-Alfvén and
the drift waves and will soon be used to confirm and extend the present
knowledge beyond the FLR approximation.
In parallel, a new electromagnetic model for macro-instabilities has
been derived for a future version of the PENN code, keeping
the complete parallel dynamics of passing bulk- and energetic ions
together with large
[46];
the model retains the mode conversion both to the kinetic-Alfvén and
the drift waves and will soon be used to confirm and extend the present
knowledge beyond the FLR approximation.
In parallel, a new electromagnetic model for macro-instabilities has
been derived for a future version of the PENN code, keeping
the complete parallel dynamics of passing bulk- and energetic ions
together with large 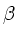 and arbitrary shape in the limit of small
Larmor radii.
A complete derivation for the current perturbation along the magnetic field
will be given elsewhere, but finally results in an integro-differential
expression in configuration space that can be written symbolically as
and arbitrary shape in the limit of small
Larmor radii.
A complete derivation for the current perturbation along the magnetic field
will be given elsewhere, but finally results in an integro-differential
expression in configuration space that can be written symbolically as
![\begin{displaymath}
\begin{split}
j_\Vert = \frac{i\omega}{4\pi}&\left\{-\frac{c...
...B}B_\Vert\right]
\right) +\mathrm{drifts} \right\}
\end{split}\end{displaymath}](img70.gif) |
(10) |
The kernel
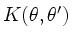 clearly plays an essential role here,
since it contains the wave-particle resonances that are integrated
numerically over
clearly plays an essential role here,
since it contains the wave-particle resonances that are integrated
numerically over  and couples different poloidal locations
through the integral operator.
Finite Larmor radius corrections appear explicitly with the second order
operators
and couples different poloidal locations
through the integral operator.
Finite Larmor radius corrections appear explicitly with the second order
operators
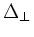 and inhomogeneities with the drift frequency
and inhomogeneities with the drift frequency
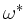 .
Resonant effect from energetic particles are not shown here,
but are also kept in the small Larmor radius approximation.
The physics we hope to study with this new model ranges down in frequency
from the energetic-particle-kinetic AEs, drift-kinetic AEs, beta-induced
AEs and finally the non-ideal counterparts of MHD instabilities such as
KBMs, internal kink and resistive-wall modes.
.
Resonant effect from energetic particles are not shown here,
but are also kept in the small Larmor radius approximation.
The physics we hope to study with this new model ranges down in frequency
from the energetic-particle-kinetic AEs, drift-kinetic AEs, beta-induced
AEs and finally the non-ideal counterparts of MHD instabilities such as
KBMs, internal kink and resistive-wall modes.


 Previous: Ad-hoc complex resistivity
Up: GLOBAL MODES & DAMPING
Next: CONCLUSIONS
© André JAUN, Alfvén Laboratory, Royal Institute of Technology, Stockholm
Previous: Ad-hoc complex resistivity
Up: GLOBAL MODES & DAMPING
Next: CONCLUSIONS
© André JAUN, Alfvén Laboratory, Royal Institute of Technology, Stockholm
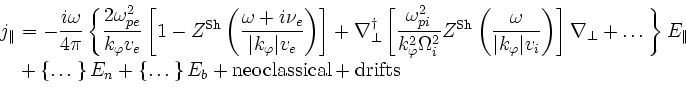


 Previous: Ad-hoc complex resistivity
Up: GLOBAL MODES & DAMPING
Next: CONCLUSIONS
Previous: Ad-hoc complex resistivity
Up: GLOBAL MODES & DAMPING
Next: CONCLUSIONS
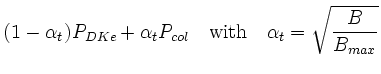
![]() .
Five conversion mechanisms have been found so far, of which four occur to
the kinetic Alfvén wave and only two had been expected from heuristic
arguments. They are illustrated in the sketch of Fig.3:
.
Five conversion mechanisms have been found so far, of which four occur to
the kinetic Alfvén wave and only two had been expected from heuristic
arguments. They are illustrated in the sketch of Fig.3:
![\includegraphics[height=6cm]{FIG/torMDCV.eps}](img65.gif)
![]() plasmas in simple toroidal
geometry and includes the parallel dynamics of passing and trapped bulk
particles to all orders in
plasmas in simple toroidal
geometry and includes the parallel dynamics of passing and trapped bulk
particles to all orders in
![]() [46];
the model retains the mode conversion both to the kinetic-Alfvén and
the drift waves and will soon be used to confirm and extend the present
knowledge beyond the FLR approximation.
In parallel, a new electromagnetic model for macro-instabilities has
been derived for a future version of the PENN code, keeping
the complete parallel dynamics of passing bulk- and energetic ions
together with large
[46];
the model retains the mode conversion both to the kinetic-Alfvén and
the drift waves and will soon be used to confirm and extend the present
knowledge beyond the FLR approximation.
In parallel, a new electromagnetic model for macro-instabilities has
been derived for a future version of the PENN code, keeping
the complete parallel dynamics of passing bulk- and energetic ions
together with large ![]() and arbitrary shape in the limit of small
Larmor radii.
A complete derivation for the current perturbation along the magnetic field
will be given elsewhere, but finally results in an integro-differential
expression in configuration space that can be written symbolically as
and arbitrary shape in the limit of small
Larmor radii.
A complete derivation for the current perturbation along the magnetic field
will be given elsewhere, but finally results in an integro-differential
expression in configuration space that can be written symbolically as


 Previous: Ad-hoc complex resistivity
Up: GLOBAL MODES & DAMPING
Next: CONCLUSIONS
© André JAUN, Alfvén Laboratory, Royal Institute of Technology, Stockholm
Previous: Ad-hoc complex resistivity
Up: GLOBAL MODES & DAMPING
Next: CONCLUSIONS
© André JAUN, Alfvén Laboratory, Royal Institute of Technology, Stockholm